Calculus: Graphical, Numerical, Algebraic introduces the three core approaches to understanding calculus, integrating visual, computational, and symbolic methods. This guide helps students solve problems effectively.

The Graphical Approach in Calculus
The graphical approach in calculus involves analyzing functions through graphs, enabling visualization of limits, continuity, and derivatives. This method supports problem-solving and aligns with AP exam preparation.
2.1. Understanding Functions Through Graphs
Graphs provide a visual representation of functions, making it easier to identify key features such as increasing or decreasing intervals, concavity, and points of inflection. By analyzing graphs, students can understand the behavior of functions, including asymptotes, intercepts, and transformations. This approach helps in connecting graphical representations with numerical and algebraic interpretations, fostering a deeper understanding of function relationships. Exercises in resources like Calculus: Graphical, Numerical, Algebraic emphasize interpreting and sketching graphs to solve real-world problems, aligning with AP calculus standards and enhancing problem-solving skills.
2.2. Visualizing Limits and Continuity
Graphical methods allow students to visualize limits and continuity, essential concepts in calculus. By analyzing function graphs, learners identify behavior as variables approach specific points. Limits are visually represented by examining the function’s trend near a value, while continuity is assessed by checking for breaks, jumps, or holes. Graphs empower students to intuitively grasp these ideas, making abstract definitions more concrete. Resources like Calculus: Graphical, Numerical, Algebraic provide exercises to interpret graphical behavior, reinforcing the connection between visual insights and algebraic definitions, and preparing students for advanced problem-solving in calculus.
2.3. Graphical Interpretation of Derivatives and Integrals
The graphical approach provides a intuitive understanding of derivatives and integrals. Derivatives are interpreted as the slope of tangent lines to a function’s graph, revealing rates of change and concavity. Integrals are visualized as the area under a curve, representing accumulation. Graphs help identify key features like maxima, minima, and inflection points, while also illustrating concepts like net area and average value. This visual method enhances problem-solving skills and connects algebraic definitions to real-world applications, making calculus more accessible for students learning through graphical representations.

The Numerical Approach in Calculus
The numerical approach in calculus involves computational methods to approximate solutions for derivatives, integrals, and algebraic equations, providing practical tools for real-world problem-solving and analysis.
3.1. Evaluating Limits and Derivatives Numerically
Numerical methods provide practical tools for evaluating limits and derivatives when analytical solutions are complex or difficult to obtain. Techniques like the secant method approximate slope calculations, while numerical differentiation and integration offer alternatives to symbolic computation. These approaches are particularly useful in real-world applications where exact solutions are less accessible. By leveraging computational algorithms, students can estimate derivatives and understand limit behavior through iterative processes. Resources such as study guides and solution manuals further support mastering these numerical techniques, ensuring a comprehensive understanding of calculus fundamentals.
3.2. Numerical Integration and Estimation
Numerical integration provides methods to approximate definite integrals when exact solutions are challenging or impractical. Techniques like Riemann sums, trapezoidal rules, and Simpson’s rule estimate area under curves. These methods are essential in applied fields for solving complex integrals. Error analysis is crucial to understand the accuracy of numerical results. Resources such as study guides and solution manuals offer detailed examples and exercises to master these techniques. By combining numerical integration with graphical and algebraic approaches, students gain a comprehensive understanding of calculus applications in real-world problems.
3.3. Solving Algebraic Equations Numerically
Numerical methods are essential for solving algebraic equations that cannot be easily solved analytically. Techniques like the Newton-Raphson method and bisection method provide approximate solutions. These methods rely on iterative processes to refine estimates until convergence. Error analysis is critical to ensure accuracy. Numerical solutions are widely used in engineering and science for practical problem-solving. Resources such as study guides and solution manuals offer step-by-step examples to master these methods, emphasizing the importance of numerical approaches in calculus applications.
The Algebraic Approach in Calculus
The algebraic approach emphasizes symbolic manipulation and equation-solving, offering precise solutions to calculus problems. It builds a strong foundation for advanced mathematical reasoning and problem-solving in STEM fields.
4.1. Algebraic Manipulation of Functions
Algebraic manipulation of functions is a cornerstone of calculus, enabling precise analysis and transformation of mathematical expressions. This approach involves simplifying, factoring, and solving equations to uncover underlying patterns. By mastering techniques like polynomial expansion and rational function simplification, students gain the ability to rewrite functions in forms that reveal their behavior, such as identifying asymptotes or roots; These skills are essential for solving limits, derivatives, and integrals symbolically, aligning with the AP calculus syllabus. Clear instruction and practice exercises in resources like Calculus: Graphical, Numerical, Algebraic help students refine these algebraic strategies, ensuring a strong foundation for advanced problem-solving.
4.2. Solving Equations and Inequalities
Solving equations and inequalities is a critical algebraic skill in calculus, enabling the analysis of functions and their properties. This involves techniques such as factoring, quadratic formulas, and interval notation for inequalities. The textbook Calculus: Graphical, Numerical, Algebraic provides comprehensive guidance, ensuring students master these foundational skills. By systematically addressing linear, quadratic, and polynomial equations, as well as rational and exponential inequalities, students develop the ability to solve complex problems. Practice exercises and examples align with AP calculus standards, reinforcing the connection between algebraic manipulation and calculus applications, such as optimization and modeling real-world phenomena.
4.3. Algebraic Representation of Calculus Concepts
The algebraic approach in calculus involves translating graphical and numerical insights into symbolic representations, enabling precise mathematical formulations. This method is essential for defining limits, derivatives, and integrals algebraically, providing rigorous foundations for calculus. The textbook emphasizes the “rule of four,” integrating graphical, numerical, algebraic, and verbal methods to solve problems. Algebraic techniques, such as simplifying expressions and solving equations, are central to analyzing functions and their behavior. By mastering algebraic representations, students can tackle advanced topics like differential equations and series, bridging the gap between theoretical concepts and practical applications in fields like physics and engineering.
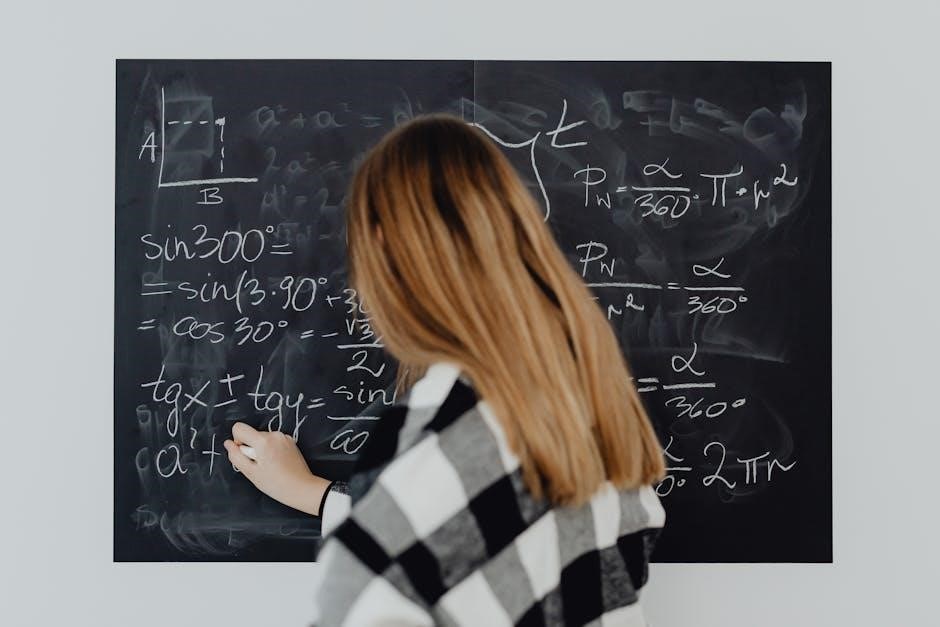
The Textbook “Calculus: Graphical, Numerical, Algebraic”
This textbook offers a comprehensive approach to calculus, blending graphical, numerical, and algebraic methods. It supports AP exams and features digital resources, guiding students to master calculus concepts effectively.
5.1. Overview of the Textbook
Calculus: Graphical, Numerical, Algebraic is a widely recognized textbook designed for high school and AP calculus students. It integrates three approaches—graphical, numerical, and algebraic—to provide a comprehensive understanding of calculus. The book aligns with the AP calculus syllabus, offering structured lessons, real-world applications, and updated examples. Its clear organization and accessible language make complex concepts manageable. The textbook is available in multiple editions, including digital formats, and is supported by online resources, study guides, and solution manuals, ensuring a well-rounded learning experience for students.
5.2. Structure and Organization
The textbook is organized into clear, logical chapters that build progressively, aligning with the AP calculus syllabus. It begins with prerequisites, followed by sections on limits, derivatives, and integrals. Each concept is explored through graphical, numerical, and algebraic methods, reinforcing understanding. The structure emphasizes real-world applications and updated examples, making abstract ideas relatable. Supplementary resources, such as study guides and online materials, are seamlessly integrated. This organized approach ensures students grasp foundational concepts and advanced topics, preparing them for exams and future studies in mathematics.
5.3; Key Features and Benefits
Calculus: Graphical, Numerical, Algebraic offers a unique blend of approaches, making complex concepts accessible. It aligns with AP syllabus changes, ensuring exam preparedness. Interactive digital resources, including graphs and numerical tools, enhance learning. The textbook provides comprehensive study guides, solution manuals, and annotated teacher editions for additional support. Its logical structure and real-world applications cater to diverse learning styles, fostering a deep understanding of calculus concepts. Regular updates and clear examples make it an invaluable resource for students and educators alike, promoting mastery of calculus through a balanced, integrated approach.

Key Concepts and Topics Covered
The textbook covers essential calculus topics, including limits, derivatives, integrals, differential equations, and series, using graphical, numerical, and algebraic methods to enhance understanding.
6.1. Limits and Continuity
The concept of limits is foundational in calculus, enabling the understanding of function behavior as inputs approach specific values. Continuity is explored through graphical, numerical, and algebraic methods, ensuring a comprehensive grasp of how functions behave without breaks or jumps; The textbook guides students in evaluating limits numerically using tables and algebraically through limit laws, while graphical interpretations visualize approaching values. Understanding continuity is tied to limits, with practical examples and exercises reinforcing these principles. This section ensures students can analyze and apply limit properties confidently, preparing them for advanced calculus topics. The integration of multiple approaches solidifies foundational knowledge effectively.
6.2. Derivatives and Their Applications
Derivatives measure rates of change and slopes of tangent lines, fundamental in understanding function behavior. The textbook introduces derivatives using graphical, numerical, and algebraic methods, ensuring a robust understanding. Graphically, students interpret slopes and analyze function increasing or decreasing. Numerically, difference quotients and derivative estimates are explored. Algebraically, rules like the power rule and chain rule are applied to find exact derivatives. Practical applications include motion along a line, related rates, and optimization problems. Examples and exercises guide students in applying derivatives to real-world scenarios, reinforcing their ability to interpret and use derivative concepts effectively. This section bridges theory with practical implementation seamlessly.
6.3. Integrals and Their Applications
Integrals represent the accumulation of quantities, such as area under curves or total change. The textbook explores integrals through graphical, numerical, and algebraic perspectives. Graphically, students interpret area and recognize the relationship between integrals and antiderivatives. Numerically, methods like Riemann sums and numerical integration are introduced; Algebraically, the Fundamental Theorem of Calculus connects differentiation and integration. Applications include calculating volumes, solving differential equations, and modeling real-world phenomena like motion and physics. Practical exercises and examples help students apply integral concepts to diverse problems, emphasizing their relevance in science, engineering, and economics. This section highlights the versatility and power of integrals in solving complex problems.
6.4. Differential Equations and Series
Differential equations model rates of change, while series represent sums of infinite sequences. The textbook introduces these concepts through graphical, numerical, and algebraic methods. Graphically, students analyze slope fields and solution curves. Numerically, methods like Euler’s algorithm approximate solutions. Algebraically, power series and Taylor expansions are explored. Applications include modeling population growth, heat transfer, and vibrational systems. The section emphasizes the interplay between calculus concepts and real-world problems, providing practical tools for solving complex mathematical and scientific challenges. Exercises and examples guide students in mastering these advanced techniques, essential for fields like physics and engineering. Series are also used to approximate functions, enabling deeper analysis of calculus problems. This chapter bridges theoretical foundations with practical implementation, preparing students for advanced studies and applications.
Resources and Supplements
The textbook offers digital access, PDF versions, and online resources. Study guides and solution manuals provide additional support, enhancing understanding of calculus concepts through graphical, numerical, and algebraic methods.
7.1. PDF Versions and Digital Access
The textbook Calculus: Graphical, Numerical, Algebraic is available in PDF format, offering flexibility for digital learning. Students can access the entire book online, with features like searchable text and zoom capabilities. The PDF version is ideal for devices like tablets and laptops, enabling portability and convenience. Digital access also includes interactive simulations, practice problems, and video tutorials, enhancing the learning experience. This format ensures that students can study anywhere, anytime, while retaining all the benefits of the print edition. The PDF version is a valuable resource for both classroom and self-paced learning environments.
7.2. Online Companion Resources
The online companion resources for Calculus: Graphical, Numerical, Algebraic provide a comprehensive suite of tools to enhance learning. These include interactive simulations, video tutorials, and practice problems with step-by-step solutions. Students can access graphing tools to visualize functions and explore calculus concepts dynamically. Additionally, data analysis features and pre-built templates help with numerical computations. The online platform also offers a study guide and solution manual, further supporting independent study. These resources are designed to deepen understanding and improve problem-solving skills, making them an invaluable supplement to the textbook.
7.3. Study Guides and Solution Manuals
The study guides and solution manuals complement the textbook by providing detailed explanations and solutions to exercises. These resources help students master key concepts through practice problems and step-by-step solutions. The guides include chapter summaries, additional examples, and tips for understanding complex topics. Solution manuals offer answers to odd and even numbered problems, enabling self-assessment and reinforcement of learning. These resources are particularly useful for independent study and exam preparation, ensuring a thorough understanding of calculus concepts and their applications.

Applications of Calculus
Calculus applies to real-world problems in physics, engineering, economics, and computer science, enabling modeling, optimization, and problem-solving. It prepares students for advanced studies and practical applications.
8.1. Real-World Applications
Calculus is fundamental in solving real-world problems across various fields, including physics, engineering, economics, and computer science. Its methods, such as optimization, rates of change, and accumulation, are used to model population growth, fluid dynamics, and economic trends. Engineers apply calculus to design structures and systems, while physicists use it to describe motion and energy. In computer science, calculus aids in algorithm development and machine learning. These applications highlight the practical relevance of calculus, bridging theoretical concepts with tangible solutions. The graphical, numerical, and algebraic approaches provide versatile tools for addressing complex challenges in diverse disciplines.
8.2. Preparation for Advanced Placement (AP) Exams
The textbook “Calculus: Graphical, Numerical, Algebraic” is tailored to prepare students for Advanced Placement (AP) exams, aligning with the AP calculus syllabus. It emphasizes problem-solving techniques, essential for tackling AP exam questions. The book integrates graphical, numerical, and algebraic methods, ensuring a comprehensive understanding of key concepts like limits, derivatives, and integrals. With updated examples, exercises, and digital resources, it equips students with practical skills and theoretical knowledge. The AP Edition includes annotated teacher resources and study guides, making it an ideal tool for exam preparation and success in AP calculus courses.
Calculus: Graphical, Numerical, Algebraic offers a comprehensive and integrated approach to learning calculus, blending visual, computational, and symbolic methods. By aligning with AP syllabus changes, it ensures students are well-prepared for exams. The textbook’s logical structure, updated examples, and digital resources make complex concepts accessible. Its focus on problem-solving and the “rule of four” equips students with versatile skills. This guide is invaluable for building a strong foundation in calculus, making it an essential resource for both classroom learning and independent study. It truly exemplifies a holistic approach to mastering calculus.

